1 树的结构
1.1 树的逻辑结构
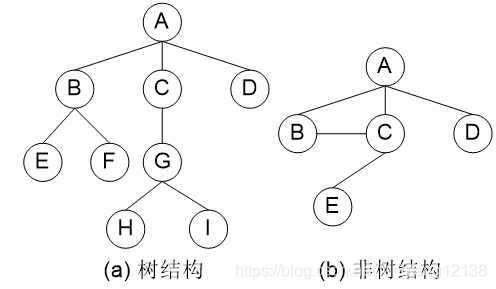
1) 树的定义与特点
| 说明 | ||
|---|---|---|
| 树 | 子树、空树、有序树、无序树、森林 | 空树无结点,有序无序看子树交换顺序是不是同一棵 |
| 点 | 叶子结点、分支结点、根结点、孩子结点、双亲结点、兄弟结点、堂兄弟结点 | |
| 度 | 结点的度、树的度 | 度即分叉数,最大的结点的度即树的度 |
| 路 | 路径长度、祖先、子孙 | 分支数为路径长度,路径若存在必唯一 |
| 层 | 结点的层数、树的深度/高度 | 层数从1开始 |
| 结点的层序编号 | 从上到下、从左到右、从1开始、连续自然数编号 |
2) 树的遍历
前序遍历:从根结点,从左到右前序遍历子树,ABEFCGHID
后序遍历:从叶子结点,从左到右后序遍历子树,EFBHIGCDA
层序遍历:按层序编号,ABCDEFGHI
1.2 树的存储结构
1) 双亲表示法:每个结点,除自身数据外,还记录双亲结点的下标,方便求解双亲,但求结点的孩子需要遍历。
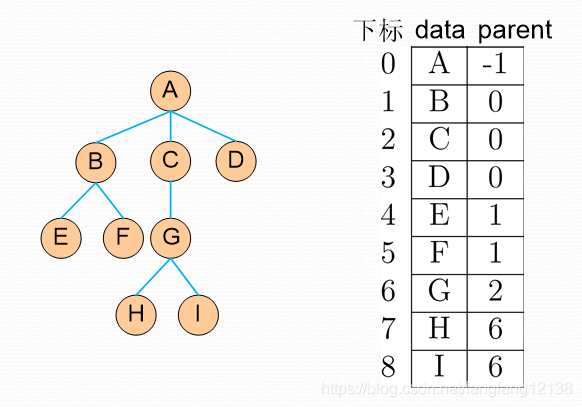
2) 孩子链表表示法:每个结点,除自身数据外,还记录一个链表,链表记录从左到右孩子结点的下标,优缺点有双亲表示法相反
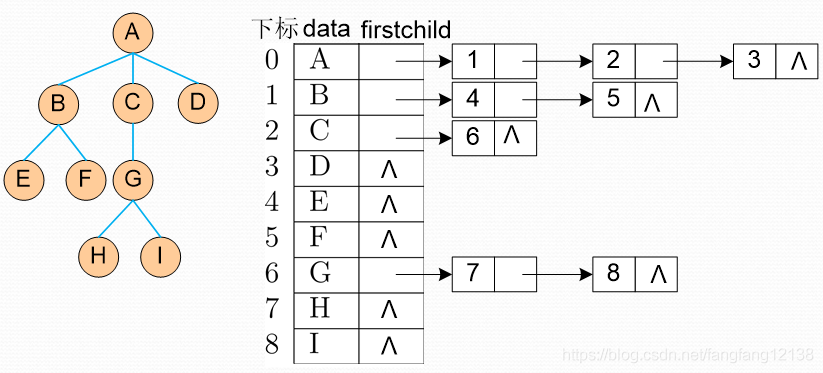
3) 孩子兄弟表示法:每个结点,除自身数据外,还记录第一个孩子结点和右侧的第一个兄弟结点
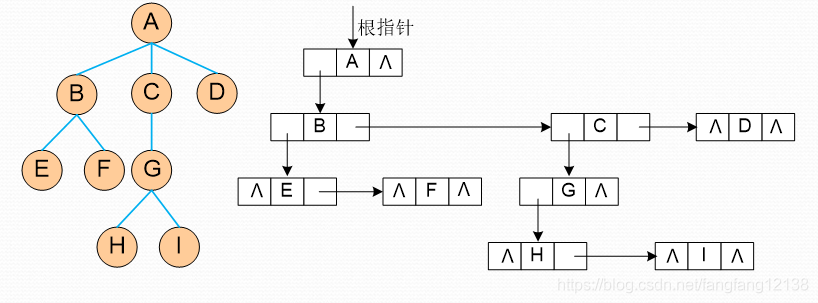
1.3 二叉树的逻辑结构
1) 二叉树的定义与说明
| 说明 | ||
|---|---|---|
| 二叉树 | 左子树、右子树、空二叉树 | 左右子树互不相交,结点的度最大为2 |
| 斜树 | 左斜树、右斜树 | 所有分支都只有左子树/右子树,斜树 =》结点个数等于树的深度 |
| 满二叉树 | 所有分支结点都有左右子树,所有叶子结点都在同一层 | |
| 完全二叉树 | 按层序编号,倒序从满二叉树中去掉任意数量结点,满二叉树=》完全二叉树 |
2) 二叉树的性质
3) 二叉树的遍历
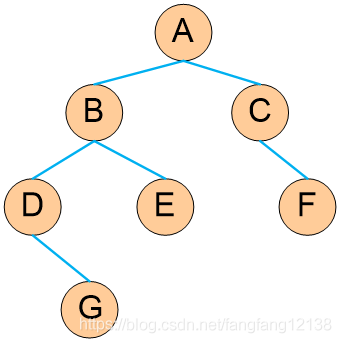
前序遍历:从根结点,从左到右前序遍历左右子树,ABDGECF
中序遍历:先遍历根结点的左子树,访问根结点,遍历右子树,DGBEACF ,在遍历子树的过程中,也是按照:先左,然后结点,然后右,(NDGBEANCF)
后序遍历:从叶子结点,从左到右后序遍历左右子树,GDEBFCA
层序遍历:按层序编号,ABCDEFG
1.4 二叉树的存储结构(递归遍历)
1) 顺序存储结构
根据层序编号,使用一维数组存储。适用于完全二叉树,对于非完全二叉树,需要补充空结点生成完全二叉树,存在空间浪费的情况,特别是右斜树。
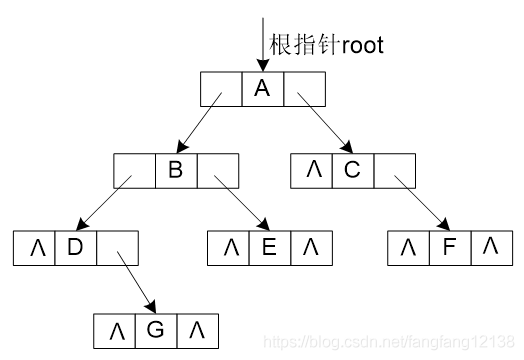
2) 二叉链表
对比树结构的孩子链表示法,结点使用二叉链表,每个结点包括数据域 和 左右两个指针域指向左右分支结点。
(二叉链表的遍历、构造和析构都可以递归的方式进行,以结点指针为空作为结束标志)
(二叉链表的构造:将二叉树进行扩展,使得原二叉树的结点的度都是2,然后再递归创建)
| pLeftChild | data | pRightChild |
|---|
template <class T>
struct BiNode{
T data;
BiNode<T> *lchild, *rchild;
};
//构造
template <class T>
BiNode<T> *BiTree<T>::Creat(BiNode<T> *bt)
{
char ch;
cout<<"请输入创建一棵二叉树的结点数据:"<<endl;
cin>>ch;
/*'#'代表空二叉树*/
if(ch == '#')
return NULL;
else
{
bt = new BiNode<T>; /*生成新结点*/
bt->data = ch;
bt->lchild = Creat(bt->lchild); /*递归创建左子树*/
bt->rchild = Creat(bt->rchild); /*递归创建右子树*/
}
return bt;
}
//析构
template <class T>
void BiTree<T>::Release(BiNode<T> *bt)
{
/*按照后序遍历的顺序释放二叉树*/
if(bt != NULL)
{
Release(bt->lchild); /*释放左子树*/
Release(bt->rchild); /*释放右子树*/
delete bt; /*删除根结点*/
}
}
//前序遍历
template <class T>
void BiTree<T>::PreOrder(BiNode<T> *bt)
{
if(bt == NULL) /*递归调用的边界条件*/
return;
else
{
cout<<bt->data<<" "; /*访问根结点*/
PreOrder(bt->lchild); /*前序递归遍历左子树*/
PreOrder(bt->rchild); /*前序递归遍历右子树*/
}
}
//中序遍历
template <class T>
void BiTree<T>::InOrder(BiNode<T> *bt)
{
if(bt == NULL)
return; /*递归调用的边界条件*/
else
{
InOrder(bt->lchild); /*中序递归遍历左子树*/
cout<<bt->data<<" "; /*访问根结点*/
InOrder(bt->rchild); /*中序递归遍历的右子树*/
}
}
//后序遍历
template <class T>
void BiTree<T>::PostOrder(BiNode<T> *bt)
{
if(bt == NULL)
return; /*递归调用的边界条件*/
else
{
PostOrder(bt->lchild); /*后序递归遍历左子树*/
PostOrder(bt->rchild); /*后序递归遍历右子树*/
cout<<bt->data<<" "; /*访问根结点*/
}
}
//层序遍历
template <class T>
void BiTree<T>::LevelOrder(BiNode<T> *bt)
{
BiNode<T> *q;
queue<BiNode<T> *> Q;
if(bt == NULL)
return;
else
{
Q.push(bt); /*bt入队*/
/*队列非空时循环*/
while(Q.empty() != 1)
{
q = Q.pop(); /*队头出队*/
cout<<q->data<<" "; /*访问队头*/
if(q->lchild != NULL) /*如果队头有左孩子,左孩子入队*/
Q.push(q->lchild);
if(q->rchild != NULL) /*如果队头有右孩子,右孩子入队*/
Q.push(q->rchild);
}
}
}
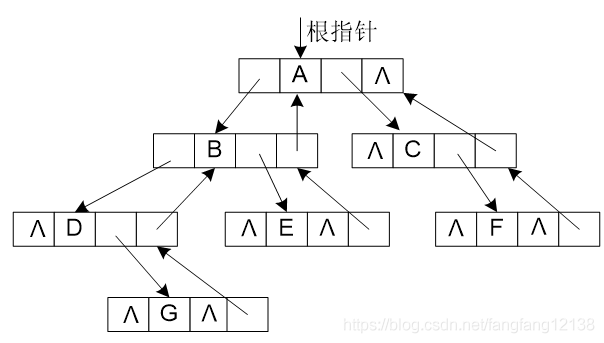
3) 三叉链表
在二叉链表的基础上,增加指向双亲结点的指针。
| pLeftChild | data | pRightChild | pParent |
|---|
2 二叉树应用
2.1 非递归遍历二叉树
//前序
template <class T>
void BiTree<T>::preOrder(BiNode<T> *bt)
{
stack<BiNode<T> *> S;//使用栈保存访问过的结点
while(bt != NULL || S.empty() != 1)
{
while(bt != NULL)
{
cout<<bt->data<<endl;
S.push(bt);
bt = bt->lchild;
}
if(S.empty() != 1)
{
bt = S.pop();
bt = bt->rchild;
}
}
}
//中序
template <class T>
void BiTree<T>::inOrder(BiNode<T> *bt)
{
stack<BiNode<T> *> S;//使用栈保存访问过的结点
while(bt != NULL || S.empty() != 1)
{
while(bt != NULL) //bt == NULL 说明左子树为空,或左子树已访问完
{
S.push(bt);
bt = bt->lchild;
}
if(S.empty() != 1)
{
bt = S.pop();
cout<<bt->data<<endl;//先打印左子树,再打印结点
bt = bt->rchild;
}
}
}
//后序1:使用标志位,给结点绑定一个flag,访问完左子树,flag为1,左右子树都访问完后,flag为2
template <class T>
void BiTree<T>::postOrder(BiNode<T> *bt)
{
stack<Element> S;
Element e;
/*bt不为空或者栈不为空*/
while(bt != NULL || S.Empty() == 0)
{
while(bt != NULL)
{
e.ptr = bt;
e.flag = 1;
S.posh(e);
bt = bt->lchild;
}
/*栈不为空并且栈顶的flag为2时,出栈并访问*/
while((S.empty() != 1)&&(S.top()).flag == 2)
{
e = S.Pop();
cout<<e.ptr->data<<" ";
}
/*栈不为空,并且栈顶的flag为1时,将栈顶的flag更改为2,并访问其右孩子*/
if(S.empty() != 1)
{
e = S.pop();
bt = e.ptr->rchild;
e.flag = 2;
S.push(e);
}
}
}
//后序2:不使用标志位
template <class T>
void BiTree<T>::postOrder(BiNode<T> *bt)
{
stack<BiNode<T> *> s;
stack<BiNode<T> *> output;
s.push(bt);
while (!s.empty())
{
bt = s.pop();
output.push(bt);
if (bt->lchild)
s.push(bt->lchild);
if (bt->rchild)
s.push(bt->rchild);
}
while (!output.empty())
{
bt = output.pop();
cout << bt->data << " ";
}
}2.2 重建二叉树
//由前序序列和中序序列
template <class T>
BiNode<T>* BiTree<T>::Rebuild(T *preOrder, T *inOrder, int n)
{
if(n == 0)
return NULL;
T c = preOrder[0];/*获得前序遍历的第一个结点*/
BiNode<T> *node = new BiNode<T >;/*创建根结点*/
node->data = c;
node->lchild = NULL;
node->rchild = NULL;
int i;
for(i = 0; i < n && inOrder[i] != c; i++)/*在中序遍历序列中寻找根结点的位置*/
;
int lenLeft = i;/*左子树结点个数*/
int lenRight = n - i - 1; /*右子树结点个数*/
if(lenLeft > 0)/*左子树不为空,递归重建左子树*/
node->lchild = Rebuild(&preOrder[1], &inOrder[0], lenLeft);
if(lenRight > 0) /*右子树不为空,递归重建右子树*/
node->rchild = Rebuild(&preOrder[lenLeft+1], &inOrder[lenLeft+1], lenRight);
return node;
}
//由后序序列和中序序列
template <class T>
BiNode<T>* BiTree<T>::Rebuild(T *postOrder, T *inOrder, int n)
{
if(n == 0)
return NULL;
T c = postOrder[n-1];/*获得后序遍历的最后一个结点*/
BiNode<T> *node = new BiNode<T>; /*创建根结点*/
node->data = c;
node->lchild = NULL;
node->rchild = NULL;
int i;
for(i = 0; i < n && inOrder[i] != c; i++)/*在中序遍历序列中寻找根结点的位置*/
;
int lenLeft = i;/*左子树结点个数*/
int lenRight = n - i - 1; /*右子树结点个数*/
if(lenLeft > 0)/*左子树不为空,重建左子树*/
node->lchild = Rebuild(&postOrder[0], &inOrder[0], lenLeft);
if(lenRight > 0)/*右子树不为空,重建右子树*/
node->rchild = Rebuild(&postOrder[lenLeft], &inOrder[lenLeft+1], lenRight);
return node;
}3 二叉搜索树 / 堆 / 红黑树
系列参考
1) 《数据结构(C++)边学边做》任平红等著
2) 《剑指offer》何海涛著
3) http://bookshadow.com/weblog/2015/01/19/binary-tree-post-order-traversal/
