1 图的结构
1.1 图的逻辑结构
- 图(graph)由顶点(vertex)的非空集合和顶点之间的边(edge)的集合组成。
| 边 | 无向(undirected)边、有向边 |
| 图 | 无向图、有向图、稠密(dense)图、稀疏(sparse)图 、子图(subgraph) |
| 简单图 | 不存在顶点到自身的边,不存在重复出现的边 |
| 完全图 | 任意两顶点存在边,无向完全图(数量为 (n-1)n/2 )、有向完全图(双向 数量为 (n-1)n ) |
| 邻接与依附 | 无向:顶点互为邻接(adjacent)点,边依附(adhere)于两顶点;有向:起点邻接到终点,终点是起点的邻接点 |
| 度 | 无向:依附于顶点的边的数量;有向:出度(作为起点)、入度(作为终点) |
| 权值与网 | 权值(weight):边的意义;网:带权值的图(有向网、无向网) |
| 路径 | 路径、路径长度、回路(路径起终点相同)、简单路径(无重复顶点)、简单回路(只重复起终点) |
| 连通图 连通分量 | 无向图中,任意两顶点存在路径;非连通图的极大连通子图为连通分量 |
| 强连通图 强连通分量 | 有向图中,任意两顶点双向存在路径;非强连通图的极大强连通子图为强连通分量 |
| 生成树 | 连通图的极小连通子图(n个顶点和最少的边)、有向图的子图(全部顶点且仅一顶点入度为0,其余入度为1) |
| 生成森林 | 连通分量的生成树,组成森林 |
- 遍历的方式
♥ 寻找邻接点
♥ 设置访问标志,避免重复访问
♥ 多个邻接点选择方式不同,分为深度优先(推荐使用栈)和广度优先(推荐使用队列)
1.2 图的存储结构
邻接矩阵(栅格)
- 深度优先遍历
//1、初始化各顶点未被访问 for(int i=0;i<vertexNum;i++) visited[i]=0; //2、第一个顶点入栈 stack<int> st; for(int i=0;i<vertexNum;i++) if(visited[i]==0) { st.push(i); DFS(st.top()); st.pop(); } //3、递归 void DFS(int v) { visited[v]=1; //确认已遍历 for(int i=0;i<vertexNum;i++) { if((visited[i]==0) && (arc[v][i]==1))//找到该顶点的邻接点 { st.push(i); DFS(st.top()); st.pop(); } } } - 广度优先遍历
//1、初始化各顶点未被访问 for(int i=0;i<vertexNum;i++) visited[i]=0; //2、第一个顶点入队 queue<int> que; for(int i=0;i<vertexNum;i++) if(visited[i]==0) { que.push(i); visited[i]=1; break; } //3、循环:依次入队,依次处理 while(!que.empty()) { int v = que.front(); for(int i=0;i<vertexNum;i++) { if((visited[i]==0) && (arc[v][i]==1))//找到该顶点的邻接点 { que.push(i); visited[i]=1; } } que.pop(); }
1.3 测试程序
邻接矩阵 深度优先遍历
针对无向连通图。
#include <iostream>
#include <stack>
using namespace std;
int vertexNum=5;
int visited[5]={0};
int arc[5][5]={0,1,0,1,1, //邻接矩阵
1,0,1,0,1,
0,1,0,0,0,
1,0,0,0,0,
1,1,0,0,0};
stack<int> st;
void DFS(int v)
{
visited[v]=1; //确认已遍历
for(int i=0;i<vertexNum;i++)
{
if((visited[i]==0) && (arc[v][i]==1))//找到该顶点的邻接点
{
st.push(i);
cout<<"push:"<<i<<" "<<st.size()<<endl;
DFS(st.top());
st.pop();
cout<<"pop:"<<i<<" "<<st.size()<<endl;
}
}
}
int main()
{
//1、初始化各顶点未被访问
for(int i=0;i<vertexNum;i++)
visited[i]=0;
//2、第一个顶点入栈
for(int i=0;i<vertexNum;i++)
{
if(visited[i]==0)
{
st.push(i);
cout<<"push:"<<i<<" "<<st.size()<<endl;
DFS(st.top());
st.pop();
cout<<"pop:"<<i<<" "<<st.size()<<endl;
}
}
}邻接矩阵 广度优先遍历
针对无向连通图。
#include <iostream>
#include <queue>
using namespace std;
int vertexNum=5;
int visited[5]={0};
int arc[5][5]={0,1,0,1,1, //邻接矩阵
1,0,1,0,1,
0,1,0,0,0,
1,0,0,0,0,
1,1,0,0,0};
int main()
{
//1、初始化各顶点未被访问
for(int i=0;i<vertexNum;i++)
visited[i]=0;
//2、第一个顶点入队
queue<int> que;
for(int i=0;i<vertexNum;i++)
if(visited[i]==0)
{
que.push(i);
visited[i]=1;
cout<<"push:"<<i<<" "<<que.size()<<endl;
break;
}
//3、循环:依次入队,依次处理
while(!que.empty())
{
int v = que.front();
cout<<"front:"<<que.front()<<" "<<que.size()<<endl;
for(int i=0;i<vertexNum;i++)
{
if((visited[i]==0) && (arc[v][i]==1))//找到该顶点的邻接点
{
que.push(i);
visited[i]=1;
cout<<"push:"<<i<<" "<<que.size()<<endl;
}
}
que.pop();
}
}2 最小生成树
2.1 最小生成树(MST,minimal spanning tree)
无向连通网的生成树中,权值代价最小的生成树,称为最小权重生成树,简称最小生成树。
(无向图,连通图,权值与网,生成树)
应用:n个城市之间铺设电缆,目标使得任意两个城市互通,不同城市之间铺设电缆代价不同,求代价最小的铺设方法。这是一道面试题:(
2.2 Prim算法
基本思想
- 设无向连通网 G=(V,E) ,最小生成树 T=(U,TE)
- T 初值: U={v0} ,v0∈V,TE 为空
- 重复:
对每一个 V-U 中的顶点(设n个顶点),遍历 U 中顶点,找到一条最短边,n个顶点形成一个候选最短边集
在候选最短边集中,找到最最短的一条边
把 V-U 中的这一点,放入 U ,同时,把对应边放入 TE ,直到 V 和 U 相等。 - 算法复杂度O(n2),适于稠密连通网。
- 关键:候选最短边集(基本过程的case和代码的shortEdge数组)
基本过程
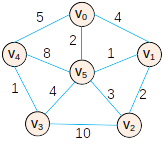 ————————->
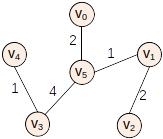
————————->
- 初始状态
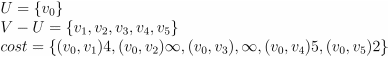
- 将点 v5 和边 (v0,v5)2 加入最小生成树
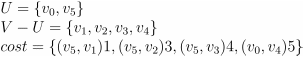
- 将点 v1 和边 (v5,v1)1 加入最小生成树
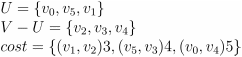
- 将点 v2 和边 (v1,v2)2 加入最小生成树
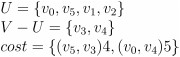
- 将点 v3 和边 (v5,v3)4 加入最小生成树
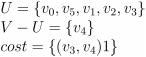
- 将点 v4 和边 (v3,v4)1 加入最小生成树
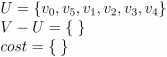
代码(非测试)
//1、初始化辅助数组,辅助数组用于标记 V-U中顶点 到 U中顶点 的 最短代价和对应顶点,功能类似于基本过程中的cost
for(int i=1;i<vertexNum;i++)
{
//初始取v0加入集合U,因此最短代价依次是与v0的代价值,对应顶点为i和v0
shortEdge[i].lowcost = arc[0][i]; //V-U中顶点 到 U中顶点 的最短代价
shortEdge[i].adjvex = 0; //V-U中顶点 到 U中顶点 的对应顶点
}
//2、加入集合的方式
shortEdge[0].lowcost = 0; //代价为0时,认为改顶点已经在最小生成树中了,这里v0已经在其中了
//3、循环
for(int i=1;i<vertexNum;i++) //这里是循环vertexNum-1次,每次添加一个顶点到U
{
//3.1、根据辅助数组确定最最短边
int k; //最最短边对应的 V-U中顶点
for(int j=1;j<vertexNum;j++) //初始化k
if(shortEdge[j].lowcost != 0)
{ k=j; break; }
for(int j=1;j<vertexNum;j++) //更新k
if(shortEdge[j].lowcost != 0 && shortEdge[j].lowcost < shortEdge[k].lowcost)
k=j;
//3.2、加入集合
shortEdge[k].lowcost = 0;
//3.3、更新辅助数组
for(int j=1;j<vertexNum;j++)
if(shortEdge[j].lowcost > arc[k][j])//比较新加入的顶点,是否代价更小(类似于RRT*的重选父节点)
{
shortEdge[j].lowcost = arc[k][j]; //V-U中顶点 到 U中顶点 的最短代价
shortEdge[j].adjvex = k; //V-U中顶点 到 U中顶点 的对应顶点
}
}
2.3 Kruscal算法
基本思想
- 设无向连通网 G=(V,E) ,最小生成树 T=(U,TE)
- T 初值: U=V ,TE 为空,即每个顶点自成一个连通分量
- 将 E 中权值有小到大排序
- 重复:
在 E 中选择最短边,判断该边的两顶点是否在两个连通分量上——边集数组
是:加入 TE
否:舍弃此边 - 算法复杂度O(elbe),适于稀疏连通网。
- 关键:边集数组,如何判断两个点是否在不同的连通分量(利用边集数组)。
基本过程
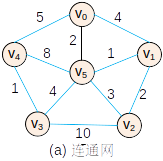 —
—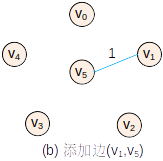 —
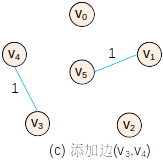
—
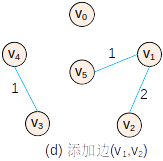 —
—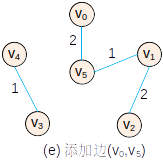 —
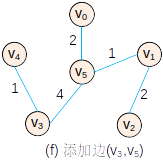
—
代码(非测试)
//1、定义、初始化、排序从小到大的边集数组
struct Edge
{
Edge(){}
Edge(int from_,int to_,int cost_,bool ok_):from(from_),to(to_),cost(cost_),ok(ok_){}
int from;
int to;
int cost;
bool ok;
};
Edge edges[edgeNum];
edges[0]=Edge{0,1,4,false};//...
bool cmp(const Edge &a,const Edge &b)
return a.cost<b.cost;
sort(edges,edges+edgeNum,cmp);//按权值排序
//2、遍历边集数组
for(int i=0;i<edgeNum;i++)
{
//2.1、判断该边的两个顶点是否在一个连通分量中
//2.2、合并两个连通分量
if(find_parent(edges[i].from)!=find_parent(edges[i].to))
{
merge(edges[i].from, edges[i].to);
edges[i].ok=true;
}
else
edges[i].ok=false;
}
2.4 测试程序
Prim算法
#include <iostream>
int vertexNum=6;
int arc[6][6]={100,4,100,100,5,2, //邻接矩阵
4,100,2,100,100,1,
100,2,100,10,100,3,
100,100,10,100,1,4,
5,100,100,1,100,8,
2,1,3,4,8,100};
struct Cost
{
int lowcost;
int adjvex;
};
int main()
{
Cost shortEdge[vertexNum];
//1、初始化辅助数组,辅助数组用于标记 V-U中顶点 到 U中顶点 的 最短代价和对应顶点,功能类似于基本过程中的cost
for(int i=1;i<vertexNum;i++)
{
//初始取v0加入集合U,因此最短代价依次是与v0的代价值,对应顶点为i和v0
shortEdge[i].lowcost = arc[0][i]; //V-U中顶点 到 U中顶点 的最短代价
shortEdge[i].adjvex = 0; //V-U中顶点 到 U中顶点 的对应顶点
}
//2、加入集合的方式
shortEdge[0].lowcost = 0; //代价为0时,认为改顶点已经在最小生成树中了,这里v0已经在其中了
//3、循环
for(int i=1;i<vertexNum;i++) //这里是循环vertexNum-1次,每次添加一个顶点到U
{
//3.1、根据辅助数组确定最最短边
int k; //最最短边对应的 V-U中顶点
for(int j=1;j<vertexNum;j++) //初始化k
if(shortEdge[j].lowcost != 0)
{
k=j; break;
}
for(int j=1;j<vertexNum;j++) //更新k
if(shortEdge[j].lowcost != 0 && shortEdge[j].lowcost < shortEdge[k].lowcost)
k=j;
std::cout<<"get vertex="<<k<<" with "<<shortEdge[k].adjvex<<",cost="<<shortEdge[k].lowcost<<std::endl;
//3.2、加入集合
shortEdge[k].lowcost = 0;
//3.3、更新辅助数组
for(int j=1;j<vertexNum;j++)
if(shortEdge[j].lowcost > arc[k][j]) //比较新加入的顶点,是否代价更小(类似于RRT*的重选父节点)
{
shortEdge[j].lowcost = arc[k][j]; //V-U中顶点 到 U中顶点 的最短代价
shortEdge[j].adjvex = k; //V-U中顶点 到 U中顶点 的对应顶点
}
}
return 0;
}Kruscal算法
#include <iostream>
#include <algorithm>
int vertexNum=6;
int edgeNum=10;
int arc[6][6]={100,4,100,100,5,2, //邻接矩阵
4,100,2,100,100,1,
100,2,100,10,100,3,
100,100,10,100,1,4,
5,100,100,1,100,8,
2,1,3,4,8,100};
int parent[6];
//边集数组
struct Edge
{
Edge(){}
Edge(int from_,int to_,int cost_,bool ok_):from(from_),to(to_),cost(cost_),ok(ok_){}
int from;
int to;
int cost;
bool ok;
};
//边集数组:成员排序方式
bool cmp(const Edge &a,const Edge &b)
{
return (a.cost) < (b.cost);
}
//幷查集:查找顶层双亲
int find_parent(int v)
{
return parent[v]==v ? v : find_parent(parent[v]);
}
//幷查集:修改顶层双亲
void merge(int from,int to)
{
parent[find_parent(to)]=find_parent(from);
}
int main()
{
//1、定义、初始化、排序从小到大的边集数组
Edge edges[edgeNum];
edges[0]=Edge{0,1,4,false};
edges[1]=Edge{0,4,5,false};
edges[2]=Edge{0,5,2,false};
edges[3]=Edge{1,2,2,false};
edges[4]=Edge{1,5,1,false};
edges[5]=Edge{2,3,10,false};
edges[6]=Edge{2,5,3,false};
edges[7]=Edge{3,4,1,false};
edges[8]=Edge{3,5,4,false};
edges[9]=Edge{4,5,8,false};
std::sort(edges,edges+edgeNum,cmp);//按权值排序
//2、初始化每个顶点的顶层双亲节点,用于判断是否在一个集合
for(int i=0;i<vertexNum;i++)
parent[i]=i;
//3、遍历边集数组
for(int i=0;i<edgeNum;i++)
{
//3.1、判断该边的两个顶点是否在一个连通分量中
//3.2、合并两个连通分量
if(find_parent(edges[i].from)!=find_parent(edges[i].to))
{
merge(edges[i].from, edges[i].to);
edges[i].ok=true;
}
else
edges[i].ok=false;
std::cout<<"get edge: from "<<edges[i].from<<" to "<<edges[i].to
<<" cost:"<<edges[i].cost<<" ok:"<<edges[i].ok<<std::endl;
for(int i=0;i<vertexNum;i++)
std::cout<<i<<" parent:"<<find_parent(i)<<std::endl;
}
return 0;
}