1、动态规划
DP问题三步走
- 定义一个动态规划数组,明确数组元素,目的是保存计算的历史记录,节省重复计算时间
- 确定数组间的关系
- 找出初始值
最大连续子序列和
有一个数组,如1, -5, 8, 3, -4, 15, -8,查找其中连续和最大的相邻串的值。
在本例中,最大值为8 + 3 + -4 + 15 = 22。- 定义动态规划数组元素:dp[i]表示到第i个元素的最大连续子序列和。
- 数组元素间的关系:dp[i] = max{ dp[i-1] + arc[i] , arc[i] },即,到第i个元素的最大连续子序列和,要么是继续累加,要么就是元素本身(重新开始一轮累加)。最终的最大值是dp数组中的最大值。(可以累加一个负数,但不能在负数上累加)
-
初始值:dp[0] = arc[0] 。
int max_successive_sub_serial_sum(int* numbers, int size) { //定义与初始化 int* dp = new int[size]; dp[0] = numbers[0]; int max_sum = dp[0]; //推算 for(int i=1;i<size;i++) { dp[i] = std::max( dp[i-1] + numbers[i] , numbers[i] ); max_sum = dp[i]>max_sum ? dp[i] : max_sum; } delete[] dp; return max_sum; } -
优化空间复杂度:只维护前后两个序列和
int max_successive_sub_serial_sum_space(int* numbers, int size) { //定义与初始化 int last_sum = numbers[0]; int max_sum = last_sum; //推算 for(int i=1;i<size;i++) { int cur_sum = std::max( last_sum + numbers[i] , numbers[i] ); max_sum = cur_sum>max_sum ? cur_sum : max_sum; last_sum = cur_sum; } return max_sum; }
二维网格与路径
一个 m x n 的二维网格,从左上角移动到右下角,一共多少种路径,每次只能向右或向下移动一格。- 定义动态规划数组元素:dp[ i ][ j ] 是到达第 i 行第 j 列的路径总数,i 和 j 从0开始。
- 数组元素间的关系:dp[ i ][ j ] = dp[ i – 1 ][ j ] + dp[ i ][ j – 1 ],即这一点可以由上面网格和左侧网格抵达,路径总数为两路之和
-
初始值:dp[ 0 ][ 0 ] … dp[ 0 ][ n-1 ] = 1,dp[ 0 ] … dp[ 0 ][ m-1 ][ 0 ] = 1,最左侧和最上面的网格都只有一条路径。
int unique_path(int rows, int cols) { //定义与初始化 int** dp = new int*[rows]; for(int i=0;i<rows;i++) { dp[i] = new int[cols]; memset(dp[i],0,cols); //memset是逐字节初始化,因此只有0和-1是正常初始化 } for(int i=0;i<cols;i++) dp[0][i]=1; for(int i=0;i<rows;i++) dp[i][0]=1; //推算 for(int i=1;i<rows;i++) for(int j=1;j<cols;j++) dp[i][j] = dp[i-1][j] + dp[i][j-1]; //输出 int sum = dp[rows-1][cols-1]; for(int i=0;i<rows;i++) delete[] dp[i]; delete[] dp; return sum; } -
优化空间复杂度:只保存一行的记录,然后不断迭代
int unique_path_space(int rows, int cols) { //定义与初始化 int* dp = new int[cols]; for(int i=0;i<cols;i++) dp[i] = 1; //推算 for(int i=1;i<rows;i++) for(int j=1;j<cols;j++) dp[j] = dp[j] + dp[j-1]; //输出 int sum = dp[cols-1]; delete[] dp; return sum; }
二维网格与路径2 最短路径
一个 m x n 的二维网格,从左上角移动到右下角,求最短路径长度,每次只能向右或向下移动一格。- 定义动态规划数组元素:dp[ i ][ j ] 为到达第 i 行第 j 列的最短路径。
- 数组元素间的关系:dp[ i ][ j ] = min{ dp[ i – 1 ][ j ] + arc[ i ][ j ] , dp[ i ][ j-1 ] + arc[ i ][ j ] }。
-
初始值:
dp[ 0 ][ 0 ] = arc[ 0 ][ 0 ]
dp[ 0 ][ j ] = dp[ 0 ][ j – 1 ] + arc[ 0 ][ j ]
dp[ i ][ 0 ] = dp[ i – 1 ][ 0 ] + arc[ i ][ 0 ]int unique_path_shortest(int** map, int rows, int cols ) { //定义与初始化 int** dp = new int*[rows]; for(int i=0;i<rows;i++) { dp[i] = new int[cols]; memset(dp[i],0,cols); } dp[0][0] = map[0][0]; for(int i=1;i<cols;i++) dp[0][i] = dp[0][i-1] + map[0][i]; for(int i=1;i<rows;i++) dp[i][0] = dp[i-1][0] + map[i][0]; //推算 for(int i=1;i<rows;i++) for(int j=1;j<cols;j++) dp[i][j] = std::min(dp[i-1][j] + map[i][j] , dp[i][j-1] + map[i][j]); //输出 int sum_shortest = dp[rows-1][cols-1]; for(int i=0;i<rows;i++) delete[] dp[i]; delete[] dp; return sum_shortest; } -
优化空间复杂度:只保存一行的记录,然后不断迭代
int unique_path_shortest_space(int** map, int rows, int cols ) { //定义与初始化 int* dp = new int[cols]; dp[0] = map[0][0]; for(int i=1;i<cols;i++) dp[i] = dp[i-1] + map[0][i]; //推算 for(int i=1;i<rows;i++) { dp[0] = dp[0] + map[i][0]; for(int j=1;j<cols;j++) dp[j] = std::min(dp[j] + map[i][j] , dp[j-1] + map[i][j]); } //输出 int sum_shortest = dp[cols-1]; delete[] dp; return sum_shortest; }
最长递增子序列(LIS)
2、排序
| 排序 | 插入排序 | 冒泡排序 | 归并排序 | 快速排序 |
|---|---|---|---|---|
| 基本思想 | 自第二个记录开始,有序前插 | 相邻元素比较,逆序交换,逐遍把最大值移至最后 | 相邻两个/多个顺序表合并,初始每个元素都是一个顺序表 | 两侧依次扫描,将轴值移至正确位置 |
| 时间复杂度 | n~n^2 | n~n^2 | nlbn | nlbn~n^2 |
| 平均时间复杂度 | n^2 | n^2 | nlbn | nlbn |
| 空间复杂度 | 1 | 1 | n | lbn~n |
| 应用/优化 | 适用于元素数量少,且基本有序,改进:分割,分别直插,基本有序后全体直插 | 双向起泡 | 相邻-一趟-递归 | 递归次数-空间复杂度 |
快速排序
将待排数组不断分成两部分,分别排序
int partition(int arr[], int start, int end)
{
int mid = arr[start];
int i = start;
int j = end;
while(i<j){
//右侧扫描,将小于轴值的元素移到左侧
while(i<j && arr[j]>mid)
j--;
if(i<j){
arr[i] = arr[j];
i++;
}
//左侧扫描,将大于轴值的元素移到右侧
while(i<j && arr[i]<mid)
i++;
if(i<j){
arr[j] = arr[i];
j--;
}
}
arr[i] = mid;
return i;
}
void quick_sort(int arr[], int start, int end)
{
int mid_index = partition(arr, start, end);
if(start < mid_index)
quick_sort(arr, start, mid_index-1);
if(mid_index < end)
quick_sort(arr, mid_index+1,end);
}3、查找
二分查找
复杂度 lgn
bool binary_search(int arr[], int length, int num)
{
int start = 0;
int end = length-1;
int mid = (start+end)/2;
while(start<=end)
{
if(arr[mid]==num)
return true;
else if(arr[mid]>num)
end = mid - 1;
else
start = mid + 1;
mid = (start+end)/2;
}
return false;
}二叉排序树
复杂度 lgn~n
myNode* searchSortBiTree(myNode* root, int k)
{
if(root == nullptr)
return nullptr;
else if(root->data == k)
return root;
else if(root->data > k)
return searchSortBiTree(root->leftChild, k);
else
return searchSortBiTree(root->rightChild, k);
}4、二叉树
struct myNode
{
int data;
myNode* leftChild;
myNode* rightChild;
int flag;
};树的构造与释放
按层序遍历的方式构造。
myNode* createBiTree(int values[], int length)
{
queue<myNode*> nodes;
int cnt = 0;
myNode* n = new myNode;
n->data = values[0];
nodes.push(n);
cnt++;
while(cnt<length)
{
myNode* top = nodes.front();
nodes.pop();
myNode* left_n = new myNode;
left_n->data = values[cnt];
nodes.push(left_n);
top->leftChild = left_n;
cnt++;
if(cnt==length)
break;
myNode* right_n = new myNode;
right_n->data = values[cnt];
nodes.push(right_n);
top->rightChild = right_n;
cnt++;
}
return n;
}
void releaseBiTree(myNode* n)
{
/*按照后序遍历的顺序释放二叉树*/
if(n != NULL)
{
releaseBiTree(n->leftChild); /*释放左子树*/
releaseBiTree(n->rightChild); /*释放右子树*/
delete n; /*删除根结点*/
}
}前序遍历
// 非递归:栈
void frontPrintBiTree(myNode* root)
{
stack<myNode*> nodes;
myNode* n = root;
while(n != nullptr || nodes.empty()!=1)
{
while(n != nullptr)
{
nodes.push(n);
cout<<n->data<<" ";
n = n->leftChild;
}
if(nodes.empty()!=1)
{
n = nodes.top();
nodes.pop();
n = n->rightChild;
}
}
}
// 递归
void frontPrintBiTree_recursion(myNode* root)
{
if(root == NULL) /*递归调用的边界条件*/
return;
else
{
cout<<root->data<<" "; /*访问根结点*/
frontPrintBiTree_recursion(root->leftChild); /*前序递归遍历左子树*/
frontPrintBiTree_recursion(root->rightChild); /*前序递归遍历右子树*/
}
}中序遍历
// 非递归:栈
void middlePrintBiTree(myNode* root)
{
stack<myNode*> nodes;
myNode* n = root;
while(n != nullptr || nodes.empty()!=1)
{
while(n != nullptr)
{
nodes.push(n);
n = n->leftChild;
}
if(nodes.empty()!=1)
{
n = nodes.top();
nodes.pop();
cout<<n->data<<" ";
n = n->rightChild;
}
}
}
// 递归
void middlePrintBiTree_recursion(myNode* root)
{
if(root == NULL) /*递归调用的边界条件*/
return;
else
{
middlePrintBiTree_recursion(root->leftChild); /*前序递归遍历左子树*/
cout<<root->data<<" "; /*访问根结点*/
middlePrintBiTree_recursion(root->rightChild); /*前序递归遍历右子树*/
}
}后序遍历
void backPrintBiTree(myNode* root)
{
stack<myNode*> nodes;
myNode* n = root;
while(n!=nullptr || nodes.empty()!=1)
{
while(n != nullptr)
{
n->flag = 1;
nodes.push(n);
n = n->leftChild;
}
while(nodes.empty()!=1 && nodes.top()->flag==2)
{
n = nodes.top();
nodes.pop();
cout<<n->data<<" ";
if(n==root)
return;
}
if(nodes.empty()!=1)
{
n = nodes.top();
n->flag = 2;
n = n->rightChild;
}
}
}
// 递归
void backPrintBiTree_recursion(myNode* root)
{
if(root == NULL) /*递归调用的边界条件*/
return;
else
{
backPrintBiTree_recursion(root->leftChild); /*前序递归遍历左子树*/
backPrintBiTree_recursion(root->rightChild); /*前序递归遍历右子树*/
cout<<root->data<<" "; /*访问根结点*/
}
}层序遍历
void levelPrintBiTree(myNode* root)
{
queue<myNode*> nodes;
myNode* n = root;
nodes.push(n);
while(nodes.empty()!=1)
{
n = nodes.top();
nodes.pop();
cout<<n->data<<" ";
if(n->leftChild != nullptr)
nodes.push(n->leftChild);
if(n->rightChild != nullptr)
nodes.push(n->rightChild);
}
}Z字遍历
void ZPrintBiTree(myNode* root)
{
queue<myNode*> nodes_que;
stack<myNode*> nodes_sta;
int line = 1;
int cnt = 0;
queue<myNode*> nodes;
myNode* n = root;
nodes.push(n);
while(nodes.empty()!=1)
{
//层序遍历
n = nodes.front();
nodes.pop();
if(n->leftChild != nullptr)
nodes.push(n->leftChild);
if(n->rightChild != nullptr)
nodes.push(n->rightChild);
//Z字遍历
cnt++;
if(line%2 == 1)
{
nodes_que.push(n);
if(cnt==pow(2,line-1))
{
line++;
cnt=0;
while(nodes_que.empty()!=1)
{
cout<<nodes_que.front()->data<<" ";
nodes_que.pop();
}
}
}
else
{
nodes_sta.push(n);
if(cnt==pow(2,line-1))
{
line++;
cnt=0;
while(nodes_sta.empty()!=1)
{
cout<<nodes_sta.top()->data<<" ";
nodes_sta.pop();
}
}
}
}
//没打印的打印完
while(nodes_que.empty()!=1)
{
cout<<nodes_que.front()->data<<" ";
nodes_que.pop();
}
while(nodes_sta.empty()!=1)
{
cout<<nodes_sta.top()->data<<" ";
nodes_sta.pop();
}
}重建二叉树:前序+中序
myNode* createBiTreeByFrontMid(int* frontValues, int* midValues, int length)
{
if(length==0)//只针对第一次使用
return nullptr;
myNode* root = new myNode;//确定这一段的根节点,然后划分左右两子树
root->data = frontValues[0];
root->leftChild = nullptr;
root->rightChild = nullptr;
int i;
for(i=0;i<length && midValues[i]!=frontValues[0];i++)
;
int leftLength = i;
int rightLength = length-i-1;
if(leftLength>0)
root->leftChild = createBiTreeByFrontMid(&frontValues[1], &midValues[0], leftLength);
if(rightLength>0)
root->rightChild = createBiTreeByFrontMid(&frontValues[leftLength+1], &midValues[leftLength+1], rightLength);
return root;
}重建二叉树:中序+后序
myNode* createBiTreeByBackMid(int* backValues, int* midValues, int length)
{
if(length==0)//只针对第一次使用
return nullptr;
myNode* root = new myNode;//确定这一段的根节点,然后划分左右两子树
root->data = backValues[length-1];
root->leftChild = nullptr;
root->rightChild = nullptr;
int i;
for(i=0;i<length && midValues[i]!=backValues[length-1];i++)
;
int leftLength = i;
int rightLength = length-i-1;
if(leftLength>0)
root->leftChild = createBiTreeByBackMid(&backValues[0], &midValues[0], leftLength);
if(rightLength>0)
root->rightChild = createBiTreeByBackMid(&backValues[leftLength], &midValues[leftLength+1], rightLength);
return root;
}二叉排序树
二叉排序树:空树或非空树,非空树满足左子树所有节点小于根节点,右子树所有节点大于根节点,左右子树又是二叉排序树。
插入
void insertSortBiTree(myNode* &root, myNode* newNode)
{
if(root==nullptr)
root = newNode;
else if(root->data > newNode->data)
insertSortBiTree(root->leftChild, newNode);
else
insertSortBiTree(root->rightChild, newNode);
}构造
myNode* createSortBiTree(int data[], int n)
{
myNode* root = nullptr;
myNode* newNode;
for(int i=0;i<n;i++)
{
newNode = new myNode;
newNode->data = data[i];
newNode->leftChild = nullptr;
newNode->rightChild = nullptr;
insertSortBiTree(root, newNode);
}
return root;
}5、队列与栈
两个队列实现栈
class myStack
{
private:
queue<int> que1;
queue<int> que2;
public:
myStack();
~myStack(){};
void push(int);
void pop();
int top();
};
myStack::myStack(){}
void myStack::push(int data)//在非空的队列末尾添加新元素
{
if(que1.empty())
que2.push(data);
else
que1.push(data);
}
void myStack::pop()//将非空队列元素转移到空队列,留最后一个弹出
{
if(que1.empty() && que2.empty())
return ;
if(que1.empty())
{
while(que2.size()!=1)
{
que1.push(que2.front());
que2.pop();
}
que2.pop();
}
else
{
while(que1.size()!=1)
{
que2.push(que1.front());
que1.pop();
}
que1.pop();
}
}
int myStack::top()//将非空队列元素转移到空队列,最后一个输出
{
if(que1.empty() && que2.empty())
return -1;
int out;
if(que1.empty())
{
while(que2.size()!=1)
{
que1.push(que2.front());
que2.pop();
}
out = que2.front();
que1.push(out);
que2.pop();
}
else
{
while(que1.size()!=1)
{
que2.push(que1.front());
que1.pop();
}
out = que1.front();
que2.push(out);
que1.pop();
}
return out;
}两个栈实现队列
class myQueue
{
private:
stack<int> sta1;//存
stack<int> sta2;//取
public:
myQueue();
~myQueue(){};
void push(int);
void pop();
int front();
};
myQueue::myQueue(){}
void myQueue::push(int data)
{
sta1.push(data);
}
void myQueue::pop()
{
if(sta1.empty())
return ;
while(sta1.size()!=1)
{
sta2.push(sta1.top());
sta1.pop();
}
sta1.pop();
while(sta2.size()!=0)
{
sta1.push(sta2.top());
sta2.pop();
}
}
int myQueue::front()
{
if(sta1.empty())
return -1;
while(sta1.size()!=1)
{
sta2.push(sta1.top());
sta1.pop();
}
int out = sta1.top();
sta2.push(out);
sta1.pop();
while(sta2.size()!=0)
{
sta1.push(sta2.top());
sta2.pop();
}
return out;
}循环队列*
相对于直线队列来讲,直线队列在元素出队后,头指针向后移动,导致删除元素后的空间无法在利用,即使元素个数小于空间大小,依然无法再进行插入,即所谓的“假上溢”。当变成循环队列之后,删除元素后的空间仍然可以利用,最大限度的利用空间。
6、图
深度优先遍历
void DFS_recursion(int curVertex, int vertexNum, vector<int>* arc, vector<int>* visited)
{
(*visited)[curVertex] = 1; //标记该次遍历的顶点
cout<<curVertex<<" ";
for(int i=0; i<vertexNum;i++) //遍历该顶点连接的其他顶点
if((*visited)[i]==0 && (*arc)[curVertex*vertexNum+i]==1)
DFS_recursion(i, vertexNum, arc, visited);
}
void DFS(int vertexNum, vector<int>* arc)
{
//初始化所有顶点未被遍历
vector<int> visited;
for(int i=0;i<vertexNum; i++)
visited.push_back(0);
//深度遍历
for(int i=0; i<vertexNum; i++)//从第i个顶点开始的一个连通分量
{
if(visited[i]==0)
DFS_recursion(i, vertexNum, arc, &visited);
}
}广度优先遍历
void BFS(int vertexNum, vector<int>* arc)
{
//初始化所有顶点未被遍历
vector<int> visited;
for(int i=0;i<vertexNum; i++)
visited.push_back(0);
//广度遍历
queue<int> q;
for(int i=0;i<vertexNum; i++)//从第i个顶点开始的一个连通分量
{
if(visited[i]==0)
{
q.push(i);
visited[i]=1;
while(q.empty()!=1)
{
int v = q.front();
q.pop();
cout<<v<<" ";
for(int j=0; j<vertexNum; j++)
if(visited[j]==0 && (*arc)[v*vertexNum+j]==1)
{
q.push(j);
visited[j]=1;
}
}
}
}
}最小生成树
n个城市之间铺设电缆,目标使得任意两个城市互通,不同城市之间铺设电缆代价不同,求代价最小的铺设方法。
Prim
向最小生成树添加点。
void Prim(int vertexNum, vector<int>* arc)
{
//初始化候选最短边集
vector<int> connectCost; //候选最短边集:候选顶点到正式顶点的最小代价 代价为0,即选为正式顶点
vector<int> connectVertex; //候选最短边集:最小代价对应的正式顶点 找内推?
for(int i=0;i<vertexNum;i++)
{
connectCost.push_back((*arc)[0*vertexNum + i]); //默认到自身的代价为0,因此0号顶点初始化即选为正式顶点
connectVertex.push_back(0);
}
//最小生成树:每次加入一个正式顶点,并更新候选最短边集
for(int m=1;m<vertexNum;m++)
{
//遍历最短边集,找到最最短的一个
int k=0;
for(int i=0;i<vertexNum;i++)
if(connectCost[i]!=0)
{
k=i; break;
}
for(int i=0;i<vertexNum;i++)
if(connectCost[i]!=0 && connectCost[i]<connectCost[k])
k=i;
if(connectCost[k]==0)//找一圈发现均已添加到正式顶点中,则退出
return ;
cout<<"("<<connectVertex[k]<<"->"<<k<<")-cost-"<<connectCost[k]<<" ";
//把第k个顶点加入正式顶点中
connectCost[k]=0;
//看看剩下的候选节点是不是到k的代价更小
for(int i=0;i<vertexNum;i++)
if(connectCost[i]!=0 && connectCost[i]>(*arc)[k*vertexNum + i])
{
connectCost[i] = (*arc)[k*vertexNum + i];
connectVertex[i] = k;
}
}
}Kruscal
向最小生成树添加边。
struct Edge
{
int vertexA;
int vertexB;
int cost;
};
bool cmp(const Edge &a,const Edge &b)
{
return (a.cost) < (b.cost);
}
int find_parent(int v, vector<int> &parents)
{
return parents[v]==v ? v : find_parent(parents[v], parents);//递归找到顶层双亲
}
void Kruscal(int vertexNum, vector<int>* arc)
{
//数据准备
vector<Edge> edges;
for(int i=0;i<vertexNum;i++)
for(int j=i+1;j<vertexNum;j++)
if((*arc)[i*vertexNum + j] < 100)
{
Edge edge;
edge.vertexA = i;
edge.vertexB = j;
edge.cost = (*arc)[i*vertexNum + j];
edges.push_back(edge);
}
//Kruscal
//边集数组初始化:升序排列
sort(edges.begin(),edges.end(),cmp);
//顶层双亲初始化:用于判断某一边的两顶点是否在同一个连通分量
vector<int> parents;
for(int i=0;i<vertexNum;i++)
parents.push_back(i);//初始化每个顶点自成一个连通分量,其双亲为自身
//最小生成树:每次添加一条边
for(int i=0;i<edges.size();i++)
{
//拿出一条边,判断是否在同一个连通分量:判断顶层双亲是否相同
Edge e = edges[i];
if(find_parent(e.vertexA, parents) != find_parent(e.vertexB, parents))
{
parents[find_parent(e.vertexB, parents)]=find_parent(e.vertexA, parents);
cout<<"("<<e.vertexA<<"->"<<e.vertexB<<")-cost-"<<e.cost<<" ";
}
}
}7、幷查集
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
输入格式
第一行:三个整数n,m,p,(n<=5000,m<=5000,p<=5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Mi和Mj具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
输出格式
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
- 幷查集的两种操作:查询是否在同一集合,合并不同集合
- 幷查集的思想:每个集合确定一个代表元素,形成一个树状结构,代表元素为根节点,其他元素为子节点。集合的合并就是一个集合的根节点成为另一个集合的子节点。集合的查询就是不断找父节点,直到找到根节点,判断根节点是否相同。
- 幷查集应用:最小生成树的Kruscal方法。
- 幷查集的初始化,合并和查询
int parent[NMAX] void init(int n) //初始化为本身 { for(int i=0;i<n;i++) parent[i]=i; } int find(int i) { return parent[i]==i ? i : find(parent[i]); //不断向上查询父节点,直到所属结合的根节点 } int merge(int i, int j) { parent[find(i)] = find(j);//把i所属集合的根节点,变成j所属集合根节点的子节点 } - 压缩:查询过程中将其父节点换成根节点,减少递归次数,因为只在查询时压缩,因此未必每个集合除了根节点,全是叶子节点
int find(int i) { return parent[i]==i ? i : ( parent[i] = find(parent[i]) ); //查询过程中将其父节点换成根节点 } - 按秩合并:把简单树合并到复杂树
算法学习笔记(1) : 并查集
8、字符串
有效字符串
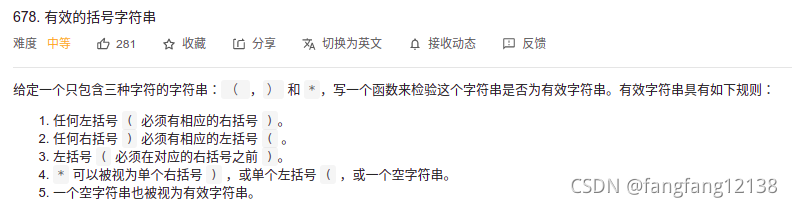
一个看着不错的答案
bool checkValidString(String s) {
int low = 0; // 表示*号都作为右括号时,左括号的数量
int hight = 0; // 表示*都作为左括号时,左括号的数量
// 如果hight < 0 说明*都作为左括号了,还是不够抵消不了右括号
// 如果low > 0 说明*号都作为右括号了,还是抵消不了括号的值
for (int i=0; i<s.length();i++){
char tmp = s.charAt(i);
if (tmp == '(') {
low++;
hight++;
}
else if (tmp == ')') {
if (low > 0) {
low--;
}
hight--;
} else if (tmp == '*') {
if (low > 0) {
low--;
}
hight++;
}
if (hight < 0) {
return false;
}
}
return low == 0;
}9、数组
差分数组 前缀和
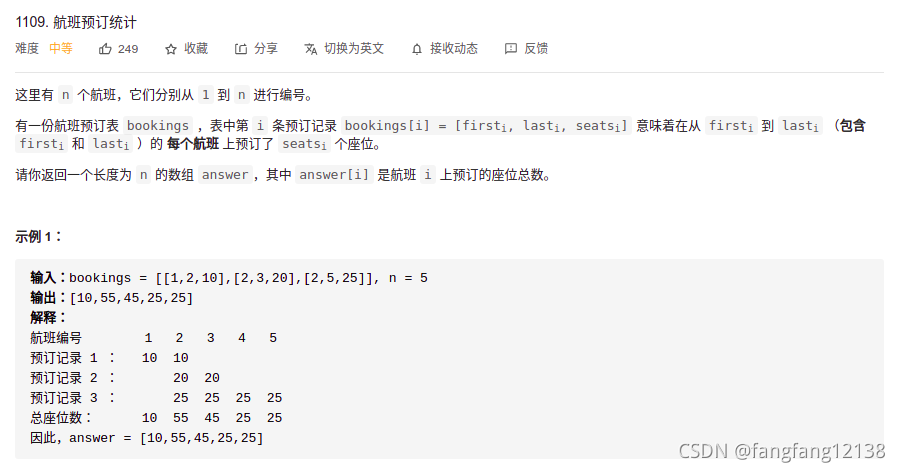
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> data;
for(int i=0; i<n;i++)
data.push_back(0);
for(auto i : bookings)
{
data[i[0]-1]+=i[2];
if(i[1]<n)
data[i[1]]-=i[2];
}
for(int i=1; i<n;i++)
data[i]+=data[i-1];
return data;
}
};测试
代码
int main()
{
//动态规划
int a[]{1,-5,8,3,-4,15,-8};
std::cout<<"max_successive_sub_serial_sum: "<<max_successive_sub_serial_sum(a,7)<<std::endl;
std::cout<<"max_successive_sub_serial_sum_space: "<<max_successive_sub_serial_sum_space(a,7)<<std::endl;
std::cout<<"unique_path: "<<unique_path(3,7)<<std::endl;
std::cout<<"unique_path_space: "<<unique_path_space(3,7)<<std::endl;
int rows=3, cols=3;
int** map = new int*[rows];
for(int i=0;i<rows;i++)
{
map[i] = new int[cols];
for(int j=0;j<cols;j++)
map[i][j]=j;
}
std::cout<<"unique_path_shortest: "<<unique_path_shortest(map, rows, cols)<<std::endl;
std::cout<<"unique_path_shortest_space: "<<unique_path_shortest_space(map, rows, cols)<<std::endl;
//排序
int arr[8]{8,7,6,5,4,4,2,1};
quick_sort(arr,0,7);
std:cout<<"quick_sort: ";
for(int i=0;i<8;i++)
std::cout<<arr[i]<<" ";
std::cout<<std::endl;
//查找
int arr1[9]{8,7,6,5,4,4,2,1,11};
std::cout<<"binary_search: "<<binary_search(arr, 8,5)<<std::endl;
std::cout<<"binary_search: "<<binary_search(arr1, 9,3)<<std::endl;
//二叉树
int arr2[9]{8,7,6,5,4,4,2,1,11};
myNode* root = createBiTree(arr2, 9);
cout<<"frontPrintBiTree: ";
frontPrintBiTree(root);
cout<<endl<<"middlePrintBiTree: ";
middlePrintBiTree(root);
cout<<endl<<"backPrintBiTree: ";
backPrintBiTree(root);
cout<<endl<<"frontPrintBiTree_recursion: ";
frontPrintBiTree_recursion(root);
cout<<endl<<"middlePrintBiTree_recursion: ";
middlePrintBiTree_recursion(root);
cout<<endl<<"backPrintBiTree_recursion: ";
backPrintBiTree_recursion(root);
cout<<endl<<"levelPrintBiTree: ";
levelPrintBiTree(root);
cout<<endl<<"ZPrintBiTree: ";
ZPrintBiTree(root);
releaseBiTree(root);
int arr2_front[9]{8,7,5,1,11,4,6,4,2};
int arr2_mid[9]{1,5,11,7,4,8,4,6,2};
int arr2_back[9]{1,11,5,4,7,4,2,6,8};
myNode* root1 = createBiTreeByFrontMid(arr2_front, arr2_mid, 9);
cout<<endl<<"createBiTreeByFrontMid backPrintBiTree: ";
backPrintBiTree(root1);
releaseBiTree(root1);
myNode* root2 = createBiTreeByBackMid(arr2_back, arr2_mid, 9);
cout<<endl<<"createBiTreeByBackMid frontPrintBiTree: ";
frontPrintBiTree(root2);
releaseBiTree(root2);
cout<<endl;
//队列与栈
myStack s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
s.push(5);
cout<<"s.top():"<<s.top()<<endl;
s.pop();
cout<<"s.top() after pop():"<<s.top()<<endl;
myQueue q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
q.push(5);
cout<<"q.front():"<<q.front()<<endl;
q.pop();
cout<<"q.front() after pop():"<<q.front()<<endl;
//图
int vertexNum = 10;
//0 1 2 3 4 5 6 7 8 9 无向图 两个连通分量
int arc_a[10][10]={0,0,1,0,1, 1,0,0,0,0,
0,0,0,1,0, 0,0,0,0,0,
1,0,0,0,0, 0,0,0,0,0,
0,1,0,0,0, 0,0,0,0,0,
1,0,0,0,0, 0,0,0,1,0,
1,0,0,0,0, 0,1,1,0,0,
0,0,0,0,0, 1,0,0,0,0,
0,0,0,0,0, 1,0,0,0,0,
0,0,0,0,1, 0,0,0,0,1,
0,0,0,0,0, 0,0,0,1,0};
vector<int> arc;
for(int i=0;i<vertexNum;i++)
for(int j=0;j<vertexNum;j++)
arc.push_back(arc_a[i][j]);
cout<<"DFS: ";
DFS(vertexNum, &arc);
cout<<endl<<"BFS: ";
BFS(vertexNum, &arc);
cout<<endl;
vertexNum = 6;
//0 1 2 3 4 5 6 7 8 9 无向连通图
int arc_b[6][6]={0, 4, 100, 100, 5, 2,
4, 0, 2, 100, 100, 1,
100, 2, 0, 10, 100, 3,
100, 100, 10, 0, 1, 4,
5, 100, 100, 1, 0, 8,
2, 1, 3, 4, 8, 0};
arc.clear();
for(int i=0;i<vertexNum;i++)
for(int j=0;j<vertexNum;j++)
arc.push_back(arc_b[i][j]);
cout<<"Prim:";
Prim(vertexNum, &arc);
cout<<endl<<"Kruscal:";
Kruscal(vertexNum, &arc);
cout<<endl;
//二叉排序树
int sortBiTree[]{80,40,70,90,100,15,81,77,89,96,1};
myNode* sortRoot = createSortBiTree(sortBiTree, 11);
cout<<"createSortBiTree frontPrintBiTree: ";
frontPrintBiTree(sortRoot);
cout<<endl;
myNode* getNode = searchSortBiTree(sortRoot, 96);
cout<<"searchSortBiTree 96:"<<(getNode!=nullptr)<<endl;
getNode = searchSortBiTree(sortRoot, 77);
cout<<"searchSortBiTree 77:"<<(getNode!=nullptr)<<endl;
getNode = searchSortBiTree(sortRoot, 2);
cout<<"searchSortBiTree 2:"<<(getNode!=nullptr)<<endl;
releaseBiTree(sortRoot);
return 0;
}输出
max_successive_sub_serial_sum: 22
max_successive_sub_serial_sum_space: 22
unique_path: 28
unique_path_space: 28
unique_path_shortest: 3
unique_path_shortest_space: 3
quick_sort: 1 2 4 4 5 6 7 8
binary_search: 1
binary_search: 0
frontPrintBiTree: 8 7 5 1 11 4 6 4 2
middlePrintBiTree: 1 5 11 7 4 8 4 6 2
backPrintBiTree: 1 11 5 4 7 4 2 6 8
frontPrintBiTree_recursion: 8 7 5 1 11 4 6 4 2
middlePrintBiTree_recursion: 1 5 11 7 4 8 4 6 2
backPrintBiTree_recursion: 1 11 5 4 7 4 2 6 8
levelPrintBiTree: 8 7 6 5 4 4 2 1 11
ZPrintBiTree: 8 6 7 5 4 4 2 11 1
createBiTreeByFrontMid backPrintBiTree: 1 11 5 4 7 4 2 6 8
createBiTreeByBackMid frontPrintBiTree: 8 7 5 1 11 4 6 4 2
s.top():5
s.top() after pop():4
q.front():1
q.front() after pop():2
DFS: 0 2 4 8 9 5 6 7 1 3
BFS: 0 2 4 5 8 6 7 9 1 3
Prim:(0->5)-cost-2 (5->1)-cost-1 (1->2)-cost-2 (5->3)-cost-4 (3->4)-cost-1
Kruscal:(1->5)-cost-1 (3->4)-cost-1 (0->5)-cost-2 (1->2)-cost-2 (3->5)-cost-4
createSortBiTree frontPrintBiTree: 80 40 15 1 70 77 90 81 89 100 96
searchSortBiTree 96:1
searchSortBiTree 77:1
searchSortBiTree 2:0