1 基础知识
1.1 编程语言
四个类型转换关键字
参考
1) static_cast
底层无const的一般静态转换,基本类型 / 具有继承关系的类型
//基本类型转换
int i = 0;
double d = static_cast<double>(i); //相当于double d = double(i);
//转换继承类的对象为基类对象
class Base{};
class Derived: public Base{};
Derived d;
Base b = static_cast<Base>(d); //相当于Base(d)2) dynamic_cast
动态转换,派生类指针(引用)转换为基类指针(引用) / 没有继承关系但被转换类有虚函数
class Base{};
class Derived: public Base{};
//派生类指针转换为基类指针
Derived *pd = new Derived;
Base *pb = dynamic_cast<Base>(pd);
//检测
if(!pb){
std::cout << "Failed Cast!";
}
//没有继承关系,但被转换类有虚函数
class A{
virtual ~A();
};
class B{};
A *pa = new A;
B *pb = dynamic_cast<B>(pa);3) const_cast
只改变const(常量)属性,不改变类型
const int *pci = 0;
//将常量转换为非常量
int *pk = const_cast<int*>(pci); //相当于int *pk = int*(pci);
const A* pca = new A;
A *pa = const_cast<A*>(pca); //相当于A *pa = A*(pca);4) reinterpret
重新解释、指针类型转换
//基本类型指针的类型转换
double d = 9.2;
double *pd = &d;
int *pi = reinterpret_cast<int*>(pd); //相当于int *pi = (int*)pd;
//不相关的类的指针类型转换
class A{};
class B{};
A *pa = new A;
B *pb = reinterpret_cast<B*>(pa); //相当于B *pb = (B*)pa;
//指针转换为整数
int *pi = 0;
long L = reinterpret_cast<long>(pi); //相当于long L = (long)pi;sizeof
1) 空类型使用sizeof,计算该类型实例的大小,使用实例,有大小,大小由编译器决定,一般是1
2) 有构造和析构函数的类型,一般也是1,实例调用这俩函数只需知道函数地址,函数地址与类型有关,与实例无关
3) 有虚函数的类型,大小为一个指针的大小(32/64->4/8),编译器会在实例中添加指向虚函数表的指针
复制构造函数
1) C++标准不允许复制构造函数进行值传递(递归溢出),允许常量引用
面试题1 赋值运算符函数
1) 返回引用(连续赋值),传入常量引用(高效、保护),释放已有内存(泄露),判断同一个实例
2) 异常安全
先释放内存还是先申请内存:内存不足的情况下,要保证原数据不变(不被提前释放),创建临时实例,构造函数new,new出来就交换,new不出来就抛出异常bad_alloc
1.2 数据结构
数组的效率
1) 静态数组:高时间效率,低空间效率
2) 动态数组:扩容操作增加时间复杂度(STL,vector)
3) 数组作为函数参数传递时,数组名将退化成同类型的指针
面试题3 数组中的重复数字
1) 题1找出重复数字,思路:把数字放到对应的下标的位置上,当发现对应位置已有该数字,则找到重复数字,对应空间O(1),时间O(n)
2) 题2不修改数组找出重复数字,思路:二分法,种类二分,确定每一段内的种类出现的次数,是否为该段的种类数。
3) 明确要求时间还是要求空间效率
面试题4 二维数组查找
1) 规律,缩小查找范围
常量字符串的地址
1) 常量字符串初始化字符数组,不同数组的地址不同,原因是不同字符数组已分配了不同位置的内存以拷贝常量字符串 P49
2) 常量字符串初始化字符指针,不同指针指向的地址相同,原因是无需重新分配内存,直接指向常量在内存中的地址
面试题5 替换空格
1) 一次移动到位,O(n),(此题不用自己扩容)
2) 考虑内存覆盖
3) 从尾部到头部,依次填入排序值
链表
1) 链表是考察重点
2) 为什么是传入指向指针的指针
要修改的是指针的内容(pHead,也就是修改一个地址),而不是修改指针指向的内容,因此传入的是指向指针的指针。
类比于,传入整型 int a 与传入其指针 int a的关系,这里是传入指针 ListNode *pHead 和指向指针的指针 ListNode **pHead。
面试题6 从尾到头打印链表
1) 栈
2) 递归 链表过长,可能导致函数调用栈溢出
void PrintListReversingly_Recursively(ListNode* pHead)
{
if(pHead != nullptr)
{
if (pHead->m_pNext != nullptr)
{
PrintListReversingly_Recursively(pHead->m_pNext);
}
printf("%d\t", pHead->m_nValue);
}
}树
1) 二叉树特例
二叉搜索树
堆
红黑树
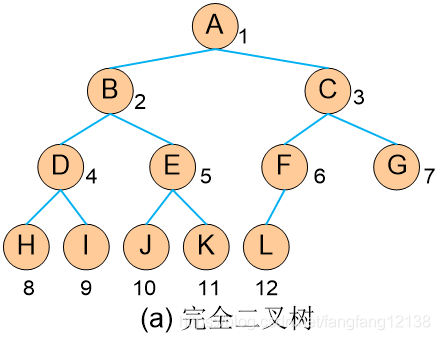
面试题7 重建二叉树
1) 已知前序和中序、或者已知后序和中序,都可以递归的形式,通过不断地 划分左右子树然后分别重建,这里方法更简洁。
面试题8 二叉树的下一个结点
1) 中序遍历:通过画图,分别考虑
2) case 1:存在右子树:下一个是其右子树的最左子结点(E -> K)
3) case 2:不存在右子树:
4) case 2.1:该结点是其父节点的左子结点,则下一个是其父节点(H -> D)
5) case 2.2:该结点是其父节点的右子结点,则下一个是向上溯源,直到溯源结点是其父节点的左子结点,则下一个是溯源结点的父节点(K -> A)
栈和队列
面试题9 用两个栈实现队列
1) 用两个队列实现栈
template <class T>
class CStack
{
public:
CStack(void);
~CStack(void);
void appendHead(const T& node);
T deleteHead();
private:
queue<T> queue1;
queue<T> queue2;
};
//入栈和出栈时,至少有一个队列为空
template <class T>
void CStack<T>::appendHead(const T& node)
{
if(0 == queue1.size()) //向非空的队列push
queue2.push(node);
else if(0 == queue2.size())
queue1.push(node);
}
template <class T>
T CStack<T>::deleteHead()
{
if(0 == queue1.size() && 0 == queue2.size())
throw new exception("stack is empty");
if(0 == queue1.size()) //从非空队列转移n-1个数据到空队列
{
while(1 != queue2.size())
{
T& data = queue2.top();
queue2.pop();
queue1.push(data);
}
T head = queue2.top();
queue2.pop();
return head;
}
else
{
while(1 != queue1.size())
{
T& data = queue1.top();
queue1.pop();
queue2.push(data);
}
T head = queue1.top();
queue1.pop();
return head;
}
}1.3 算法与数据操作
递归和循环
1) 递归优先
2) 递归,调用栈溢出,子问题重复计算
3) 自上而下的递归,可能出现子问题重复计算的问题,转而采用自下而上的循环
面试题10 斐波那契数列
1) 小青蛙,2^(n-1)
2) 覆盖矩形:f(1)=2,f(0)=0 ?
查找和排序
1) 查找重点:顺序查找、二分查找、哈希表查找、二叉排序树(二叉搜索树)
2) 排序各算法比较
| 排序 | 插入排序 | 冒泡排序 | 归并排序 | 快速排序 |
|---|---|---|---|---|
| 基本思想 | 自第二个记录开始,有序前插 | 相邻元素比较,逆序交换,逐遍把最大值移至最后 | 相邻两个/多个顺序表合并,初始每个元素都是一个顺序表 | 两侧依次扫描,将轴值移至正确位置 |
| 时间复杂度 | n~n^2 | n~n^2 | nlbn | nlbn~n^2 |
| 平均时间复杂度 | n^2 | n^2 | nlbn | nlbn |
| 空间复杂度 | 1 | 1 | n | lbn~n |
| 应用/优化 | 适用于元素数量少,且基本有序,改进:分割,分别直插,基本有序后全体直插 | 双向起泡 | 相邻-一趟-递归 | 递归次数-空间复杂度 |
3) 二分查找
bool BinarySearch(const int r[], const int length, const int searchData)
{
int start = 0;
int end = length-1;
int mid = (start+end)/2;
while(start<=end)
{
if(r[mid]==searchData)
return true;
else if(r[mid]>searchData)
end = mid - 1;
else
start = mid + 1;
mid = (start+end)/2;
}
return false;
}4) 快速排序
//进行一次排序
int Partition(int r[], int length, int start, int end)
{
if((r==nullptr) || (length<0) || (start<0) || (end>=length))
throw new std::exception("invalid parameter.");
int pivot = r[start]; //取第一个值为轴值,挖一个坑
int i = start; //左侧扫描指针
int j = end; //右侧扫描指针
while(i<j)
{
//右侧扫描:将右侧一个大值移到左侧坑位,空出一个右侧坑位
while(i<j && pivot<r[j])
j--;
if(i<j)
{
r[i] = r[j];
i++;
}
//左侧扫描:将左侧一个小值移到右侧坑位,空出一个左侧坑位
while(i<j && pivot>r[i])
i++;
if(i<j)
{
r[j] = r[i];
j--;
}
}
r[i] = pivot; //把坑位补齐
return i;
}
void QuickSort(int r[], int length, int start, int end)
{
if((r==nullptr) || (length<0) || (start<0) || (end>=length))
throw new std::exception("invalid parameter.");
if(start < end)
{
int index = Partition(r, length, start, end);
if(start < index)
QuickSort(r, length, start, index-1);
if(index < end)
QuickSort(r, length, index+1, end);
}
}面试题11 旋转数组的最小数字
1) 二分,旋转0个,顺序查找,特例
回溯法
面试题12 矩阵中的路径
#include <cstring>
void* memset( void* dest, int ch, std::size_t count );
/*
Parameters
dest - pointer to the object to fill
ch - fill byte
count - number of bytes to fill
*/1) 起始位置,for/for
2) 结束条件,‘\0’字符转结尾
3) 约束条件,不能重复走visited
4) 递归,周围四个格子
5) 回溯,pathLength–
面试题13 机器人的运动范围
动态规划与贪婪算法
1) 动态规划:
最优解问题
可分解成子问题,子问题的最优解组合起来得到整个问题的最优解
可能存在重复的子问题
自上而下分析,自下而上求解
2) 贪婪算法:数学证明
面试题14 剪绳子
位运算
1) 移位操作https://blog.csdn.net/weixin_42315600/article/details/80567944
2) 无符号数,左移右添0,右移左添0
有符号数,左移右添0,右移左补符号位
3) 移位效率高于乘除
面试题15 二进制中1的个数
1) 整数减1,再与原数与运算
2 代码质量
2.1 完整性
代码完整性
1) 测试用例
功能测试/边界测试/负面测试
2) 错误处理:返回值、全局变量、C++异常处理
/*使用异常*/
#include <iostream>
using namespace std;
int main()
{
double m, n;
cin >> m >> n;
try
{
cout << "before dividing." << endl;
if (n == 0)
throw - 1; //抛出整型异常
else if (m == 0)
throw - 1.0; //拋出 double 型异常
else
cout << m / n << endl;
cout << "after dividing." << endl;
}
catch (double d)
{
cout << "catch (double)" << d << endl;
}
catch (...) //捕获任何异常
{
cout << "catch (...)" << endl;
}
cout << "finished" << endl;
return 0;
}
/*异常再抛出:
1、不处理
如果一个函数在执行过程中拋出的异常在本函数内就被 catch 块捕获并处理,那么该异常就不会拋给这个函数的调用者(也称为“上一层的函数”);
如果异常在本函数中没有被处理,则它就会被拋给上一层的函数。
2、处理,但继续抛出,如下*/
catch (string s )
{
cout << "CountTax error : " << s << endl;
throw; //继续抛出捕获的异常,上级调用函数再次去捕获
}
/*C++标准异常类
exception 类的派生类:bad_typeid、bad_cast、bad_alloc、ios_base::failure、out_of_range...
C++ 程序在碰到某些异常时,即使程序中没有写 throw 语句,也会自动拋出上述异常类的对象。
这些异常类还都有名为 what 的成员函数,返回字符串形式的异常描述信息。*/
#include <exception> //exception类,异常类的基类
#include <stdexcept> //logic_error和runtime_error两个公派自exception的类
#include <new> //bad_alloc公派自exception的类面试题16 数值的整数次方
1) 考虑:底数为0,指数为负
2) 递归乘方
3) 位运算效率
面试题17 打印从1到最大的n位数
1) 大数问题
