在第三讲（三维空间刚体运动）这部分的3.1.2节，提到“关于平移t12，它实际对应的是坐标系1原点指向坐标系2原点的向量，在坐标系1下取的坐标，记作“从1到2的向量”，但反过来的t21，即从2指向1的向量在坐标系2下的坐标，却不等于-t12，而是和旋转还有关系”。

这里记录一下一个理解：

从相机的角度来说明可能更好理解一些。

1 相机的运动可以描述为 相对世界坐标的 旋转和平移运动的组合
2 物体在相机坐标系下和世界坐标系下的坐标值一般是不同的，假设物体在世界坐标系下的坐标和相机坐标系下的坐标如下

3 两个坐标的关系通常描述为

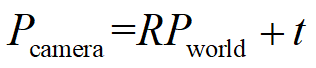
其中，R表示相机的旋转，t表示相机的平移

4 问题1：世界坐标系的原点 在相机坐标系下的表示，是t吗？显然是的。
世界坐标系原点在世界坐标系下的坐标就是一个零向量，把Pworld写作零向量代入3式即得证。

5 问题2：相机坐标系的原点 在世界坐标系下的表示，是-t吗？一般不是。
我们从空间的角度去想象，好像世界原点和相机原点，这两个点构成一个向量，“你望向我”跟“我望向你”似乎就是一个相反的关系，实际上，这种相反的关系只在某些特殊的情况下才会出现，因为我们往往不太容易去想象一个经过旋转的坐标系如何如何。
那先不想象，先从原理公式出发，看一看哪里出了问题。
我们说物体在相机和世界这两个坐标系下有不同的表示，实际上相机本身也是一个物体，相机坐标系的原点实际上就是相机本身，也就是说，Pcamera取零向量就表示了相机本身在相机坐标系的坐标（原点）。这时候，把Pcamera取零代入3中的式子，我们发现

相机的原点 在世界坐标系中的坐标并不是-t，而是附加了一个旋转，只有当旋转矩阵R为单位矩阵的时候，其坐标值才是-t。而旋转矩阵为单位矩阵，意味着，相机相对世界坐标系没有进行旋转运动。恩，没有了旋转似乎就跟我们想象的结果有些符合了（想象这东西只可意会不可言传）。

当然了，3中的式子是先旋转再平移（一般是这样），如果改成先平移再旋转，也是一样的，一般也不是相反关系。

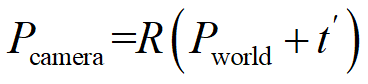
6 其他
比如，在OpenCV中solvePnP等函数计算出来的结果是按照3中的公式，即先旋转再平移，具体计算相机位置还需要一些附加的计算和转换。